君子兰萧宇的博客

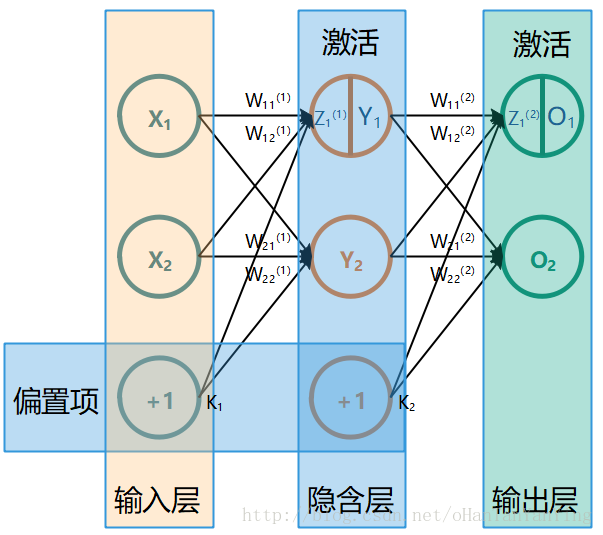
本文有一部分内容参考以下两篇文章：　　一文弄懂神经网络中的反向传播法——BackPropagation　　神经网络　　　　最简单的全连接神经网络如下图所示(这张图极其重要，本文所有的推导都参照的这张图，如果有兴趣看推导，建议保存下来跟推导一起看)： 　　它的前向传播计算过程非常简单，这里先讲一下： 前向传播 $$\begin{aligned}Y_{1} &=f\left(W_{11}^{(1)} X_{1}+W_{12}^{(1)} X_{2}+K_{1}\right) \Y_{2} &=f\left(W_{21}^{(1)} X_{1}+W_{22}^{(1)} X_{2}+K_{1}\right) \O_{1} &=f\left(W_{11}^{(2)} Y_{1}+W_{12}^{(2)} Y_{2}+K_{2}\right) \O_{2} &=f\left(W_{21}^{(2)} Y_{1}+W_{22}^{(2)} Y_{2}+K_{2}\right)\end{aligned}$$　　具体的，如果代入实际数值，取$$\begin{array ...

上一篇文章：深度学习1—最简单的全连接神经网络　　　我们完成了一个三层（输入+隐含+输出）且每层都具有两个节点的全连接神经网络的原理分析和代码编写。本篇文章将进一步探讨如何把每层固定的两个节点变成任意个节点，以方便我们下一篇文章用本篇文章完成的网络来训练手写字符集“mnist”。　　对于前向传播，基本上没有什么变化，就不用说了。主要看看后向传播的梯度下降公式。先放上上篇文章的网络图。　　上篇文章我们推知，含有两个节点的隐含层到输出层的权值对误差的偏导数，公式如下：　$$　\frac{\partial E_{总}}{\partial W_{11}^{(２)}}=(O_{1}-T_{1})*O_{1}(1-O_{1})*Y_{1}$$　　而含有两个节点的输入层到隐含层的权值对于误差梯度的偏导数公式如下：　　$$\frac{\partial E_{总}}{\partial W_{11}^{(1)}}=((O_{1}-T_{1})*O_{1}(1-O_{1})*W_{11}^{(2)}+(O_{2}-T_{2})*O_{2}(1-O_{2})*W_{21}^{(2)})*Y_{1}(1-Y_{ ...

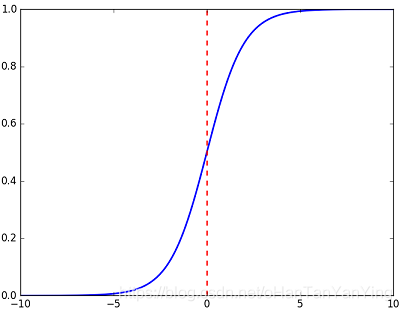
在Gan生成对抗神经网络中会用到Jensen不等式，因此做下记录。 Jensen不等式告诉我们：如果f是在区间[a,b]上的凸函数（就是导数一直增长的函数，或者说是导数的导数大于0的函数），x是随机变量，那么有：$$E(f(x))≥f(E(x))$$也就是说函数f ff的期望大于等于期望的函数。 下面来看看怎么证明，我们假设$$x_{1}, x_{2}, \ldots \ldots x_{n}$$都是区间[a,b]内的数，且$$x_{1} \leq x_{2} \leq, \ldots \ldots x_{n}$$，则上式可以写成下面这个形式：$$a_{1} f\left(x_{1}\right)+a_{2} f\left(x_{2}\right)+\ldots \ldots+a_{n} f\left(x_{n}\right) \geq f\left(a_{1} x_{1}+a_{2} x_{2}+\ldots \ldots+a_{n} x_{n}\right)$$其中$$\sum_{i=1}^{n} a_{i}=1 \text { 且 } a_{i}>0$$当n = 1时，式子 ...

上一篇文章：深度学习2—任意结点数的三层全连接神经网络　　距离上篇文章过去了快四个月了，真是时光飞逝，之前因为要考博所以耽误了更新，谁知道考完博后之前落下的接近半个学期的工作是如此之多，以至于弄到现在才算基本填完坑，实在是疲惫至极。　　另外在这段期间，发现了一本非常好的神经网络入门书籍，本篇的很多细节问题本人就是在这本书上找到的答案，强烈推荐一下： 　　 　　上篇文章介绍了如何实现一个任意结点数的三层全连接神经网络。本篇，我们将利用已经写好的代码，搭建一个输入层、隐含层、输出层分别为784、100、10的三层全连接神经网络来训练闻名已久的mnist手写数字字符集，然后自己手写一个数字来看看网络是否能比较给力的工作。　　在正式做之前，还是按照惯例讲几个会用到的知识点。 mnist数字字符集的结构解析，这个我单独写了一篇文章来做介绍了，如有需要了解请先移步：深度学习3番外篇—mnist数据集格式及转换 我们之前都是直接放入几个数作为输入，然后给网络几个数作为目标来训练网络的，而mnist手写字符集给我们的是一堆手写的2828像素的图片还有图片对应的手写数字标签，我们怎么对它进行转换？　 ...

我们简单介绍了信息熵的概念，知道了信息熵可以表达数据的信息量大小，是信息处理一个非常重要的概念。 对于离散型随机变量，信息熵公式如下：$$H ( p ) = H ( X ) = \mathrm { E } _ { x \sim p ( x ) } [ - \log p ( x ) ] = -\sum_{i=1}^n p ( x )\log p ( x )$$对于连续型随机变量，信息熵公式如下：$$H ( p ) = H ( X ) = \mathrm { E } _ { x \sim p ( x ) } [ - \log p ( x ) ] = - \int p ( x ) \log p ( x ) d x$$注意，我们前面在说明的时候log是以2为底的，但是一般情况下在神经网络中，默认以e为底，这样算出来的香农信息量虽然不是最小的可用于完整表示事件的比特数，但对于信息熵的含义来说是区别不大的。其实只要这个底数是大于1的，都能用来表达信息熵的大小。 本篇我们来看看机器学习中比较重要的一个概念—相对熵。相对熵，又被称为KL散度或信息散度，是两个概率分布间差异的非对称性度量 。在信息论中 ...

前言上回说到，通过公网IP，我们已经能使用 ip:端口 的方式，在外网访问到，我们的群晖nas了。 但是面临着两个问题。第一点，公网ip复杂难记，就是你勉强记住了，熟悉了，第二点，ip是会变化的。 这就很难受了。 有没有什么好的解决方案。 答案自然是有的——DDNS。 什么是DDNS参考百度百科。 DDNS（Dynamic Domain Name Server，动态域名服务）是将用户的动态IP地址映射到一个固定的域名解析服务上，用户每次连接网络的时候客户端程序就会通过信息传递把该主机的动态IP地址传送给位于服务商主机上的服务器程序，服务器程序负责提供DNS服务并实现动态域名解析。 这东西听起来就很符合我们的需求。 开搞。 准备其实群晖自带也是有DDNS的设置的。在，控制面板-外部访问-DDNS中。 其实，可以申请群晖自己的服务，包括域名那些。 好像是可以免费的。（没折腾过，不清楚，回头试试） 可是我为啥还是选择阿里云。 机子支持docker，想玩。（别问我为啥需要docker，因为群晖ddns的设置里面，服务商没有阿里云的） 我自己有阿里云服务器； 我已经有备案好的自己的域名了 ...

WAN远程唤醒与LAN远程唤醒有着诸多不同，WAN远程唤醒首先需要主板、网卡等硬件的支持，需要一条有效的Intelnet连接，与Lan远程唤醒不同的是，WAN远程唤醒需要经过路由器，因此下面我就来详细讲解如何在路由器上进行设置，以支持WAN远程唤醒，前提是，你已经成功进行了LAN远程唤醒。 一、WOL（远程唤醒）工具介绍 实现远程唤醒的软件有很多，原理都是相同的。下面列出几款常用的WOL软件： ■ LanHelper ■ Magic Packet Utility ■ NetWaker for windows ■ WakeOnLanGui（http://www.depicus.com） 二、准备 WAN与LAN在不同在于在广域网上，有许多的路由器等网络设备，这些设备可能会使Magic Packet的包不能到达我们想唤醒的电脑网卡上。因此，要实现通过internet来唤醒，必须得到路由器的支持。下面就以我的TP-Link WR841N无线路由为例来说明配置过程。 首先确保路由器可以正常接入internet，即通过服务商得到一个公网IP（对于家庭来说ADSL、Cable Modem是常见的上 ...

如果是连续型随机变量的情况，设p为随机变量X的概率分布，即p(x)为随机变量X在X=x处的概率密度函数值，则随机变量X在X=x处的香农信息量定义为：-$$log_2p(x)=log_2\frac{1}{p(x)}$$这时香农信息量的单位为比特。（如果非连续型随机变量，则为某一具体随机事件的概率，其他的同上） 香农信息量用于刻画消除随机变量在处的不确定性所需的信息量的大小。 上面是香农信息量的完整而严谨的表达，基本上读完就只剩下一个问题，为什么是这个式子？为了方便理解我们先看一下香农信息量在数据压缩应用的一般流程。 假设我们有一段数据长下面这样：aaBaaaVaaaaa 可以算出三个字母出现的概率分别为： $$a:\frac{10}{12}，B:\frac{1}{12}，V:\frac{1}{12}$$香农信息量为：a:0.263，B:3.585，V:3.585 也就是说如果我们要用比特来表述这几个字母，分别需要0.263，3.585，3.585个这样的比特。当然，由于比特是整数的，因此应该向上取整，变为1，4，4个比特。 这个时候我们就可以按照这个指导对字母进行编码，比如把a编码为”0 ...

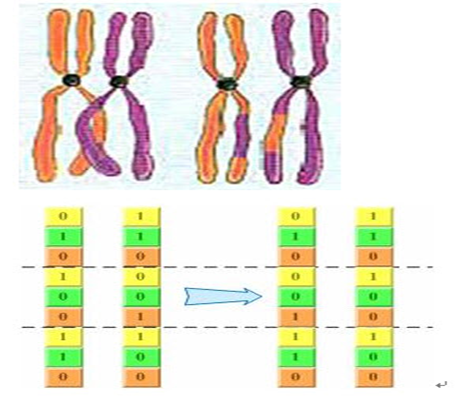
本文是去年课题组周报中的一个专题讲解，详细讲了GA，由于是周报，所以十分详细。很适合初学者入门。文中也简单提及了模拟退火算法。文章综合参考了一些互联网资料。发博客以备忘！ 三：遗传算法 ​ 照例先给出科学定义： ​ 遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。 再给出相关术语：（各位看看就好，后面都会涉及到，再细说） 基因型(genotype)：性状染色体的内部表现； 表现型(phenotype)：染色体决定的性状的外部表现，或者说，根据基因型形成的个体的外部表现； 进化(evolution)：种群逐渐适应生存环境，品质不断得到改良。生物的进化是以种群的形式进行的。 适应度(fitness)：度量某个物种对于生存环境的适应程度。 选择(selection)：以一定的概率从种群中选择若干个个体。一般， ...

项目简介本文将使用python，并借助TensorFlow框架搭建一个最简单的CNN框架，来实现对手写数字的识别。 本文搭建的CNN框架结构【1】输入层（本文的输入是一个2828且为单通道的图片，所以输入层有784个节点）【2】第一个卷积层（该卷积层包含了32个不同的55的卷积核，即该卷积层提取了32种不同图形特征，【5,5,1,32】表示卷积核尺寸为55,1个颜色通道，32个不同的卷积核）【3】第一个卷积层后的最大池化层【4】第二个卷积层（该卷积层包含了64个不同的55的卷积核，即该卷积层提取了32种不同图形特征，【5,5,32,64】表示卷积核尺寸为5*5，64个不同的卷积核）【5】第二个卷积层后的最大池化层【6】全连接层【7】一个Dropout层（为了减轻过拟合，在训练时，我们随机丢弃一部分节点的数据来减轻过拟合，预测是则保留全部数据来追求最好的预测性能）【8】Softmax层，得到最后的概率输出。【9】定义损失函数为交叉熵（cross entropy），优化器使用Adam【10】得到模型的预测精度 项目代码导入相应的库from tensorflow.examples.tutor ...