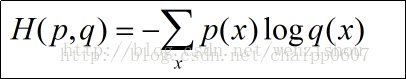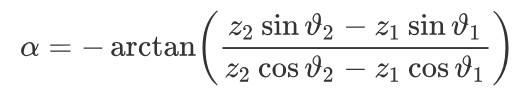君子兰萧宇的博客

在很多二分类问题中，特别是正负样本不均衡的分类问题中，常使用交叉熵作为loss对模型的参数求梯度进行更新，那为何交叉熵能作为损失函数呢，我也是带着这个问题去找解析的。 以下仅为个人理解，如有不当地方，请读到的看客能指出。 我们都知道，各种机器学习模型都是模拟输入的分布，使得模型输出的分布尽量与训练数据一致，最直观的就是MSE（均方误差，Mean squared deviation), 直接就是输出与输入的差值平方，尽量保证输入与输出相同。这种loss我们都能理解。 以下按照（1）熵的定义（2）交叉熵的定义 (3) 交叉熵的由来 （4）交叉熵作为loss的优势 作为主线来一步步理清思路。 （1）熵的定义 各种熵的名称均来自信息论领域，这方面的背景就不介绍了，随便就能找到很多。 根据维基的定义，熵的定义如下：熵是接收的每条消息中包含的信息的平均量，又被称为信息熵、信源熵、平均自信息量。直白地解释就是信息中含的信息量的大小，其定义如下： 其曲线如下所示： 可以看出，一个事件的发生的概率离0.5越近，其熵就越大，概率为0或1就是确定性事件，不能为我们带信息量。也可以看作是一件事我们越难猜测 ...

我们简单介绍了相对熵的概念，知道了相对熵可以用来表达真实事件和理论拟合出来的事件之间的差异。 相对熵的公式如下：$$D _ { K L } ( p | q ) = \sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log p \left( x _ { i } \right)-\sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log q \left( x _ { i } \right)$$可以看到前面一项是真实事件的信息熵取反，我们可以直接写成$$D _ { K L } ( p | q ) = -H(p)-\sum _ { i = 1 } ^ { N }p \left( x _ { i } \right)\log q \left( x _ { i } \right)$$在神经网络训练中，我们要训练的是$$q ( x _ { i })$$使得其与真实事件的分布越接近越好，也就是说在神经网络的训练中，相对熵会变的部分只有后面的部分，我们希望它越小越好，而前面的那部分是不变的。因此我们可以把 ...

似然（likelihood）这个词其实和概率（probability）是差不多的意思，但是在统计里面，似然函数和概率函数却是两个不同的概念。 对于函数：P(x∣θ)，输入有两个：x表示某一个具体的数据；θ表示模型的参数。 如果θ是确定的，x是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点x，其出现概率是多少。 比如我们已经知道了一个箱子里有19个黑球和一个白球，现在问你从箱子里抽出两个球，是两个黑球的概率是多少，这个时候我们的模型参数是完全知道了，就是19个黑球和一个白球，不知道的是抽出的具体的球是什么。这个时候，P(x∣θ)就是概率函数。 如果x是已知确定的，θ是变量，这个函数叫做似然函数(likelihood function)，它描述对于不同的模型参数，出现x这个样本点的概率是多少。 比如我们有一箱子球，已经从里面抽出了1个黑球8个白球，问你箱子里面黑球和白球的分布模型参数是什么。这个时候我们是不知道箱子里面的具体情况的，但我们知道抽出球的样本分布，那么我们要用样本的分布来评估箱子里的球的模型分布，这个时候P(x∣θ)就是似然函数。 ...

我们简单介绍了香农信息量的概念，由香农信息量我们可以知道对于一个已知概率的事件，我们需要多少的数据量能完整地把它表达清楚，不与外界产生歧义。但对于整个系统而言，其实我们更加关心的是表达系统整体所需要的信息量。比如我们上面举例的aaBaaaVaaaaa这段字母，虽然B和V的香农信息量比较大，但他们出现的次数明显要比a少很多，因此我们需要有一个方法来评估整体系统的信息量。 相信你可以很容易想到利用期望这个东西，因此评估的方法可以是：“事件香农信息量×事件概率”的累加。这也正是信息熵的概念。 如aaBaaaVaaaaa这段字母，信息熵为：$$-\frac{5}{6}log_2\frac{5}{6}-2×\frac{1}{12}log_2\frac{1}{12}=0.817$$abBcdeVfhgim这段字母，信息熵为：$$-12×\frac{1}{12}log_2\frac{1}{12}=3.585$$从数值上可以很直观地看出，第二段字母信息量大，和观察相一致。 对于连续型随机变量，信息熵公式变为积分的形式，如下： $$H ( p ) = H ( X ) = \mathrm { E } _ ...

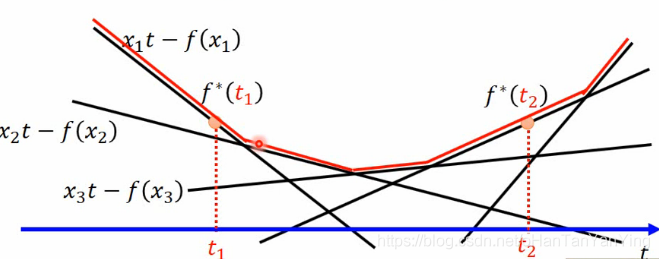
共轭函数在最近火的不行的Gan生成对抗神经网络进阶版本的数学推理中有着神奇的作用，因此在这边记录下。 共轭函数的定义为：$$f ^ { * } ( t ) = \max _ { x \in \operatorname { dom } ( f ) } { x t - f ( x ) }$$当然如果去百度它不是这么写的，但这么写和一般的写法等价。 这个公式的$$x \in \operatorname { dom } ( f )$$表示x要在f的定义域内取值，这个蛮好理解的，不在定义域内就算不了。 那它具体在干一件什么事情呢？ 可以看到式子的自变量是t，而当t定住后，式子希望在定义域内找到一个x使得右边大括号内的式子取得最大值。 它的物理意义是什么呢？ 可以看到当t定住的时候，式子其实变成了y=xt−f(x)，如果高兴也可以再把左右拆开，这样就会发现左边其实是以t为斜率的一根直线，而右边则是x的函数，那么max这货就是要找到原函数f(x)和以t为斜率的直线的最大距离点对应的$$x ^ { * }。$$ 说实在的，上面的解释我一看就懂，但完全不知所谓，心中十万只草泥马。最核心的问题在于，这个物 ...

卷积与转置卷积 得益于神经网络崛起，卷积成为近些年大热的数学词汇，不再只是待在信号处理这门要命的课程之中。 关于卷积在图像处理中的应用，操作部分看上图就明白了：假设输入图像的大小为 5 x 5，局部感受野（或称卷积核）的大小为 3 x 3，那么输出层一个神经元所对应的计算过程如上图所示。动态一点的话也可以看下面的动图。而为什么要这么算，如果学过一点图像处理就很好说明，图像处理的经典边缘提取算法如canny，sobel等，或者其他一些经典算法，其实归根结底就是一个卷积过程，只不过里面的卷积核是人为设定的而已。相比于神经网络的全连接层，用卷积层更加能够快速提取到图像的局部信息，也因此更有旋转不变性等的优势，此外需要训练的参数量相比全连接也要少的多。 在实做方面，为了效率，往往会把卷积计算用矩阵来做。 假设一个卷积操作，它的输入是 4x4，卷积核大小是 3x3，步长为 1x1，输出则为 2x2，如下所示： 我们将其从左往右，从上往下以的方式展开， 输入矩阵可以展开成维数为 [16, 1] 的矩阵，记作 x 输出矩阵可以展开成维数为 [4, 1] 的矩阵，记作 y 卷积核可以表示为 [4, ...

有时在写文章或者搞别的东西的时候需要用到别人的公式，然而一般这些公式都是复制不了的，如果这个时候一个个去打可以说相当要命。然而我们可以通过：mathpix这个神器轻轻松松解决这个问题。有了它之后，在哪看到公式直接截图就可以帮我们翻译成latex公式。就像上面这个，一截就变成了下面的这一串latex公式描述1\alpha = - \arctan \left( \frac { z _ { 2 } \sin \vartheta _ { 2 } - z _ { 1 } \sin \vartheta _ { 1 } } { z _ { 2 } \cos \vartheta _ { 2 } - z _ { 1 } \cos \vartheta _ { 1 } } \right) 接着，我们可以把这段描述放到Typora等markdown工具中，公式又将美好的出现在我们面前。当然到这里其实是不完整的。因 ...

最小二乘法 我们以最简单的一元线性模型来解释最小二乘法。什么是一元线性模型呢？ 监督学习中，如果预测的变量是离散的，我们称其为分类（如决策树，支持向量机等），如果预测的变量是连续的，我们称其为回归。回归分析中，如果只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。对于二维空间线性是一条直线；对于三维空间线性是一个平面，对于多维空间线性是一个超平面… 对于一元线性回归模型, 假设从总体中获取了n组观察值（X1，Y1），（X2，Y2）， …，（Xn，Yn）。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择： ​ （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。​ （2）用“残差绝对值和最小”确定直线位置也是 ...

我们已经了解了似然函数是什么，但怎么去把里面的θ给求出来是个更加关键的问题。这篇我们将来探讨下这个问题。 还是先举一个例子，假设有一个造币厂生产某种硬币，现在我们拿到了一枚这种硬币，想试试这硬币是不是均匀的。即想知道抛这枚硬币，正反面出现的概率（记为θ）各是多少？ 这是一个统计问题，回想一下，解决统计问题需要什么？ 数据！ 于是我们拿这枚硬币抛了10次，得到的数据x_0x0是：反正正正正反正正正反。我们想求的正面概率θ是模型参数，而抛硬币模型是二项分布(除非硬币立起来，那么这个时候要马上去买彩票，还搞什么算法)。 那么，出现实验结果x0（即反正正正正反正正正反）的似然函数是多少呢？我们是这样列式的：$$f \left( x _ { 0 } , \theta \right) = ( 1 - \theta ) \times \theta \times \theta \times \theta \times \theta \times ( 1 - \theta ) \times \theta \times \theta \times \theta \times ( 1 - \theta ) ...

海淘是什么相信大家应该都了解，在蒸蒸日上的海淘大军里，很多人在海淘购物之前担心很多问题，因此在海淘大门前徘徊许久。在没开始海淘钱我一是其中的一分子 。下面和朋友们说说亚马逊的攻略希望可以帮助那些徘徊在海淘门前的你们。 详细介绍一下在美国亚马逊购物的攻略！先给大家说一下，海淘一点都不复杂，这个教程虽然写了很长，但其实真正操作起来就几个步骤，大家不要看到这么长的教程就犹豫了！最关键的是第一次需要注册，填各种信息，所以第一次有点麻烦，有了第一次，以后海淘，就剩下爽了！（一）首先你需要准备一张信用卡,美国亚马逊支持双币信用卡、单币银联卡，都无手续费，直接以实时汇率转换成人民币结算！ (帮主现在用的最多的是浦发信用卡，海淘最高有25%的返现，平时看电影、吃饭也经常会有浦发信用卡的折扣，网上申请也非常方便 ) （二）其次对于英语不太好的亲来说，一个翻译软件是很有必要的，不过现在都有网页版的在线翻译，把要翻译的句子粘贴过去，基本解决问题。然后是换算。美国的重量采取的是磅，一磅等于454克，这样心里就有个谱了，因为运费牵扯到重量的。（三）由于大部分美国网站都不能直运回中国（美国亚马逊部分商品可直邮，直 ...